- The 30° Triangle
 |
| (http://www.gradeamathhelp.com/image-files/30-60-90-triangle.jpg) |
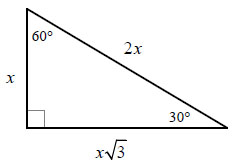
Before we begin to solve the special right triangle section of the unit circle, we must first follow the special right triangle rules as shown in the first picture. For this triangle, we start from the 30° angle and move from there. So the hypotenuse will stay the same as the 2 value, but the side opposite from our angle will be the 1 value because that is what is next to the x in our rule and the side that will be horizontal will have a set radical 3 value. We will also pretend the triangle is on a coordinate grid where the horizontal side is basically the y value and the vertical side is the x while the hypotenuse will take the radius value.
Now we can solve for this special right triangle with the parameters given. Since we are solving for a section of a unit circle, the radius always has to be one so there is one value given. To get to the value, we must divide the hypotenuse by 2 and do the same for each side. The y value becomes 1/2 and the x value becomes radical 3 over 2. The coordinates are easy to plot if you are still imagining a coordinate grid and are shown next to the corners of the triangle, with our origin starting at the 30°.
2. The 45° Triangle
 |
| (http://www.gradeamathhelp.com/image-files/45-45-90-triangle.jpg) |
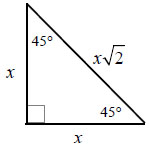
What we did previously will now be used to solve for this triangle. Now we have a 45 45 90 right triangle and we are starting from one of the 45° angles. Use the new set of special right triangle rule for this triangle and now we have to divide the hypotenuse by radical 2 to get our desired one value. Do that division for each side and now You have your x and y values as labelled in the right picture. Remember you cannot have a radical in the denominator so make sure you multiply by a radical over radical value to get rid of that radical. This time the ordered pairs are circled a midst all the work that is shown.
3. The 60° Triangle
 |
| (http://www.gradeamathhelp.com/image-files/30-60-90-triangle.jpg) |
Truth be told the resourceful learner would just use the values solved for in the 30° triangle and switch them accordingly. But an explanation will be provided for the slower learners in the crowd. We use the same rule for our 60° triangle as the first one because it is apart of the same 30,60,90 triangle, and we still divide the hypotenuse by 2 to get our desired 1 value and do the same thing for the other sides. But now we must switch the x and y values we had because the angle we are starting from is different. We must also pay careful attention to our coordinates because our values have been switched. The coordinates are circled again and the x and y values have been changed so make sure you read carefully.
4. How does this help you derive the unit circle?
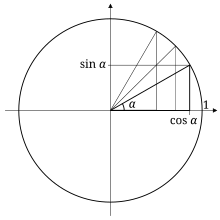
This triangle activity helped me figure out why the coordinates change as I go through a unit circle. It makes perfect sense now that I look at it, the unit circle is just composed of a bunch of triangles. The coordinate we care about is the one that is connected to the y value and the hypotenuse, that is where I figured out why we have such crazy numbers like radical 3 over 2. It also helps me remember what coordinates go where for the unit circle because now I look at the unit circle like a grid where the radius is always 1. Here is a picture I found that better illustrates the idea that these triangles fit in the unit circle.
 |
| (http://upload.wikimedia.org/wikipedia/commons/thumb/9/94/Special_right_triangles_for_trig.svg/220px-Special_right_triangles_for_trig.svg.png) |
5. What quadrant does the triangle drawn in this activity lie in? How do the values change if you draw the triangles in Quadrant II, III, or IV? Re-draw the three triangles, but this time put one of the triangles in Quadrant II, one in Quadrant III, and one in Quadrant IV. Label them as you did in the activity and describe the changes that occur.
The triangles drawn in this activity belong in quadrant I because we start from the origin and go right on the x axis and our triangle points upwards into quadrant I. The values change signs whenever we move them into other quadrants, but as long as we keep the same angle, the values will stay the same. For example the x and y value will be negative in quadrant III and only the y value will be negative in quadrant IV. Lets draw a each angle in a different spot to see these differences.
 |
| Here we have a 45° angle in quadrant II. The only thing that changes here is the sign for the x value and you can clearly see that the coordinate changes accordingly. The x and y value are labelled here to show you the difference. |
 |
| Here we have a 30° angle in quadrant III. This time both the x and the y value change signs as represented in the image, The coordinate value changes signs while in this quadrant as well. |
 |
| Here we have a 60° angle in quadrant IV and this time only the y value changes signs as seen in the labels above. |
Inquiry Activity Reflection
The coolest thing I learned from this activity was how the unit circle changes values according to rules for a triangle. I have always wondered about the similarity between triangles and circle when eating a pizza but I've never really put too much thought into it.
This activity will help me in this unit because simply put, it will make filling in the unit circle much easier. Although I still like memorizing it a lot more than this.
Something I never realized before about special right triangles and the unit circle is how closely related they are to each other. Special right triangles are the reason we have such wonky numbers in our unit circle when we are filling out the coordinates.
This activity will help me in this unit because simply put, it will make filling in the unit circle much easier. Although I still like memorizing it a lot more than this.
Something I never realized before about special right triangles and the unit circle is how closely related they are to each other. Special right triangles are the reason we have such wonky numbers in our unit circle when we are filling out the coordinates.
