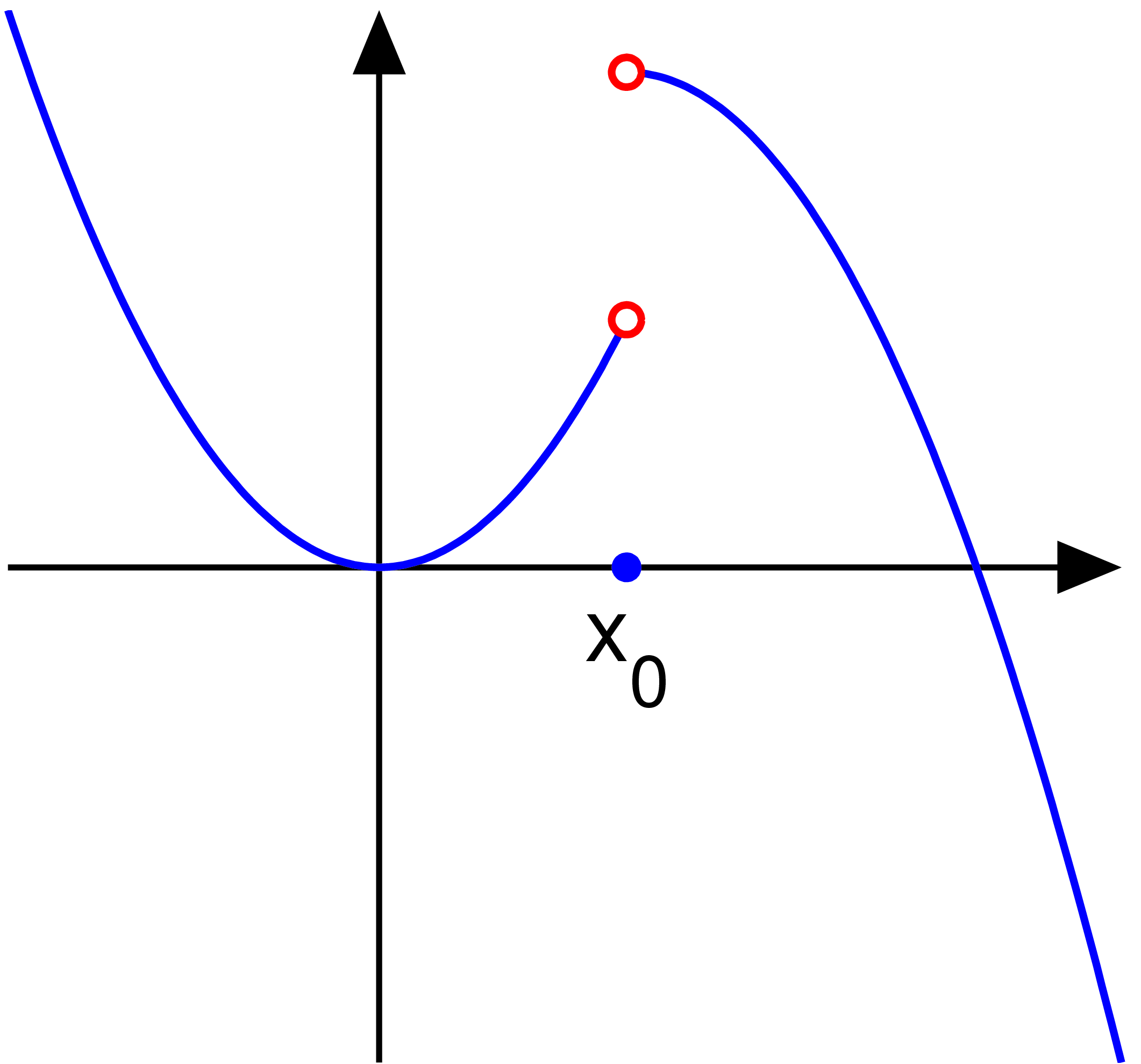
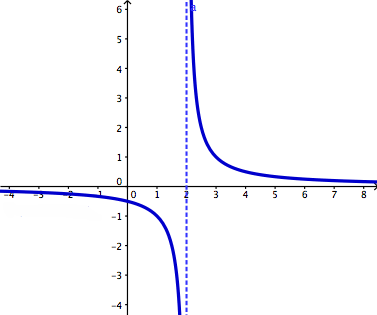
- Continuity on a graph is signified by 4 different things that we can observe. One is that a continuous graph will have no holes, jumps, breaks, or oscillating movements that may cause a discontinuity. Obviously the two are opposites of each other but can describe two different things just like we have here. To move on, a continuous graph must also be predictable, have the value and the limit be the same, and have the ability to be drawn in one continuous stroke of a pencil. Here are the four types of discontinuities that stop a continuous graph from living the good life of continuity.
 |
| http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg |
 |
| http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png |
 |
| http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif |
 |
| http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif |
2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
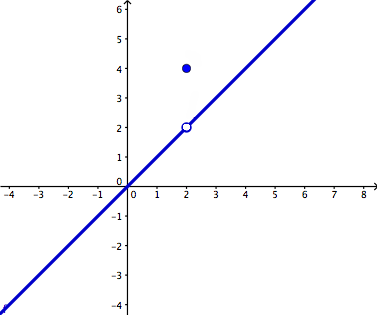
- In simple terms, a limit is an intended height that exists when a graph is continuous. A limit does not exist when there is a jump, infinite, or oscillating discontinuity. The difference between a limit and a value is that a limit is the intended height and the value is the actual height that is reached. These two can be different as seen in this graph above which has a point discontinuity. The value is the dark dot and the limit is the hole.
 |
| http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif |
3. How do we evaluate limits numerically, graphically, and algebraically?
- We evaluate limits numerically by using tables and using tenth gaps between out numbers and our limit numbers for our x and y. We evaluate limits graphically by using our two fingers to trace out the limit on the graph. And to evaluate algebraically, we employ a list of tools such as substitution, rationalizing to make substituting easier, and dividing out by the biggest x for limits at infinity.
Resources:
http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif
http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg
http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png
http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif