BQ#7: Unit V: Deriving the Difference Quotient

How do you derive the difference quotient?

• To answer this question, we must first look at a couple of formulas and remember that we are basically going from step to step in order to achieve this end result. 

(http://images.tutorvista.com/cms/images/39/difference-quotient-formula.png)

         Really the only formula we will be using in order to get to the difference quotient is the slope formula because we need to find the slope of a line that goes through two points on the function graph called the secant line.

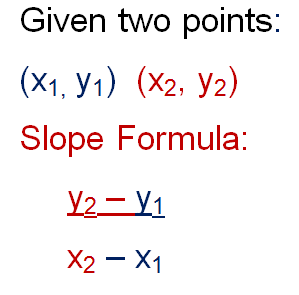(http://www.algebra-class.com/image-files/slope-formula-2.gif)

            But for now lets look at this picture and break it down to see how we get the points we need...

(http://cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG)

• On a graph of a function, assuming we don't have units labelled and all, we have no idea of knowing the exact value of those points we need. However, we can name the distance on the x-axis with a certain variable named x. Using this, we can add on this value of x with another variable that we will call h in order to get the distance to our second point on the x-axis. To get the necessary y-values, we just find the function of the x-values like we normally would with a function graph. Since we don't know the actual values, we leave both as f(x+h) and f(x). 

• The secant line is represented by these two points and now all we have to do is plug it into our slope formula to get our difference quotient. Remember that our first point is ( x, f(x)) and our second is (x+h, f(x+h)). Look back at the slope formula if you get lost. 

• Still confused? This video gives a good explanation on the entire process if you need more help.

References

http://images.tutorvista.com/cms/images/39/difference-quotient-formula.png

http://www.algebra-class.com/image-files/slope-formula-2.gif

http://cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG

https://www.youtube.com/watch?v=XA0fZh8cXV8

BQ #6: Unit U Concepts 1-8: Review

1. What is continuity? What is discontinuity?

• Continuity on a graph is signified by 4 different things that we can observe. One is that a continuous graph will have no holes, jumps, breaks, or oscillating movements that may cause a discontinuity. Obviously the two are opposites of each other but can describe two different things just like we have here. To move on, a continuous graph must also be predictable, have the value and the limit be the same, and have the ability to be drawn in one continuous stroke of a pencil. Here are the four types of discontinuities that stop a continuous graph from living the good life of continuity. 

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg

http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif

2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif

• In simple terms, a limit is an intended height that exists when a graph is continuous. A limit does not exist when there is a jump, infinite, or oscillating discontinuity. The difference between a limit and a value is that a limit is the intended height and the value is the actual height that is reached. These two can be different as seen in this graph above which has a point discontinuity. The value is the dark dot and the limit is the hole. 

3. How do we evaluate limits numerically, graphically, and algebraically?

• We evaluate limits numerically by using tables and using tenth gaps between out numbers and our limit numbers for our x and y. We evaluate limits graphically by using our two fingers to trace out the limit on the graph. And to evaluate algebraically, we employ a list of tools such as substitution, rationalizing to make substituting easier, and dividing out by the biggest x for limits at infinity. 

                               

Resources: 

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/44bad38c-431e-4382-8fe9-86303561b2a0.gif

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg

http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.png

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif

                       

BQ #4: Unit T Concept 3: Tanget and Cotangent Behavior

 

1. Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill? Use unit circle ratios to explain.

•  The reason for this behavior in a tangent graph and a cotangent graph is quite simple. It lies in the fact that tangent and cotangent have asymptotes in different spots on their graphs. This is  because tangent and cotangent graphs may have the same positive/negative pattern but since they have different ratio identities, they have different asymptotes. 
• If we remember how we get an asymptote, it is when we divide by zero and since tangent has the denominator cosine and cotangent has the denominator sine, the asymptotes will be in different spots. We can clearly see in this picture the difference between the asymptotes in both graphs. 

(http://www.analyzemath.com/trigonometry/graph_cotangent.gif)

(http://www.analyzemath.com/trigonometry/graph_tangent.gif)

 

 

 

 

References

http://www.analyzemath.com/trigonometry/graph_tangent.gif
http://www.analyzemath.com/trigonometry/graph_cotangent.gif

BQ #3: Unit T Concepts 1-3: Relations of Sin and Cos to Other Graphs

1. How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

• For these graphs we will be looking at the quadrants and the relations they have to our sine and cosine graphs. We will also be using a little bit of identities and asymptote knowledge in order to find the special relation.

• Tangent

Sine and cosine are related to the tangent graph when we are looking at the sign of the tangent graph. We know that tangent equals sine/cos as a ratio identity so if one of the graphs is negative then tangent will be negative. If both of the graphs are either positive or negative then the tangent graph will be positive.

If we look at this picture, the pattern fits perfectly for each quadrant where there is sometimes a switch in positive or negative. Watch as the tangent graph goes up or down according to its asymptotes as well.

• Cotangent

This is the same pattern for cotangent where if one is negative than cotangent is also negative. The asymptotes are in a different location but this will be gone into further detail in BQ#4.

• Secant

We are going to be looking at something different for secant and cosecant graphs. For these graphs we will only look at one of the sine and cosine graphs to find the relation between them. For a secant graph, it is related to a cosine graph because the reciprocal of cosine is secant. We can also use this information to spot where the asymptotes will be so in this case the asymptotes will be where cosine equals zero.

What we can also see from this picture is that as the cosine value on the graph goes towards zero, the secant graph will spike up to ridiculous numbers. This is because the reciprocal of a very small number or a fraction in this case equates to a very large number. We also see that when the y value equals 1 or -1 on the cosine graph, the secant graph also has that same value because the reciprocal of 1 is 1.

• Cosecant

Now for a cosecant graph, the partner we should be focusing on is the sine graph and the same reciprocal rule still applies. Of course the asymptotes will now be in different positions because we are dealing with a different graph but the same rules still apply as seen in this picture.

References

• All images screenshot from https://www.desmos.com/calculator/hjts26gwst
• http://www.schooltube.com/video/d868e626798142e4b88c/Secant%20with%20Cosine.mp4
• http://www.schooltube.com/video/0cb4440c15b14be0bcb6/CoSecant%20with%20sine.mp4

BQ #5: Unit T Concepts 1-3: Asymptotes

1. Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain

• To answer this question, we must first look at the unit circle ratios to better understand how we are getting these asymptotes.

(http://htmartin.myweb.uga.edu/6190/resources/trigfunctions.gif)

           

              Lets break this question up into two parts and answer the sine and cosine part first. If we remember correctly, an asymptote is a result of an undefined value or a value where something is divided by zero. If we look at the ratios for sine and cosine, their denominators have a very specific value called r. R will always equal one value on a unit circle which is the value of 1, and if this is the case,  we will never get asymptotes with sine and cosine. 

             Now if we look at the other four trig graphs we see that their denominators are not constant values, they may change depending on what x or y is. So these trig graphs can have asymptotes as opposed to sine and cosine. 

References

http://htmartin.myweb.uga.edu/6190/resources/trigfunctions.gif

BQ# 2: Unit T Concept Intro: Trig Graphs and the Unit Circle

1. Trig Graphs and their Relation to the Unit Circle

• Trig graphs relate to the unit circle because their signs depend on what quadrant they are in when looking at a unit circle. For example a sine function will be positive in quadrants I and II while being negative in quadrants III and IV.

     2. Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

• The period is 2pi for sine and cosine because of their pattern on the unit circle repeats after every four marks on a graph. If we measure our x-axis by pi/2 each mark, it would take a full revolution around the unit circle because it has 4 of these as quadrant angles each represent a pi/2 and for sine and cosine, the sign pattern is +,+,-,-. Which means that it won't repeat after it has passed four marks. For tangent and cotangent ,however, its pattern is +,-,+,- and you can clearly see that it repeats just by going to two marks. Two marks on our x-axis would equal to just one pi.

Look at these sine and cosine graphs for example and notice their quadrant signs and how they go all the way to pi.

(http://www.regentsprep.org/Regents/math/algtrig/ATT5/unitcirclecowine.gif)

(http://www.regentsprep.org/Regents/math/algtrig/ATT5/sine77.gif)

          Now look at these tangent and cotangent graphs and notice that they immediately start repeating just after two marks, or just pi on the x-axis. 

(http://www.analyzemath.com/trigonometry/graph_cotangent.gif)

(http://www.analyzemath.com/trigonometry/graph_tangent.gif)

              3.How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

• Sine and Cosine have amplitudes of one because they have restrictions on the range of their graphs. When we look at tangent and cotangent they go up to infinity and down to negative infinity because they don't have these restrictions. But sine and cosine have the restriction of 1 because on the Unit Circle simple because anything greater than 1 for sine and cosine is no solution. Here's an image showing the difference in range between a sine graph and a cosecant graph. 

(http://learn.roguecc.edu/mathematics/chutt/Math112/Intro/OtherTrigonometricFunctionsDay1_files/image004.png)

References

http://learn.roguecc.edu/mathematics/chutt/Math112/Intro/OtherTrigonometricFunctionsDay1_files/image004.png

http://www.analyzemath.com/trigonometry/graph_tangent.gif 

http://www.analyzemath.com/trigonometry/graph_cotangent.gif
 http://www.regentsprep.org/Regents/math/algtrig/ATT5/sine77.gif

http://www.regentsprep.org/Regents/math/algtrig/ATT5/unitcirclecowine.gif

Reflection #1: Unit Q Verifying Trig Identities

1. What does it actually mean to verify a trig identity?

• When you verify a trig identity you are basically reordering it to have it equal to whatever value you want it to equal. Think of it it like a conversion problem, to get to another unit you have to do something to the original value, maybe divide it by a certain number. When you are verifying trig identities, you are using separate identities to change your trig function into an entirely different trig expression. 

      2. What tips and tricks have you found helpful?

• The tips and tricks I have found helpful were the ones that were taught to me, there isn't really much you can learn off your own knowledge, you have to follow specific rules to these problems. These rules are like never dividing by a trig function and just knowing what strategy to use in what situation. It is like a student making up entirely different conversion factors by saying a mile now equals 5 feet, which is entirely wrong. He has to follow the given conversion factor or he will get the question wrong, so in a sense these problems are about 80% memorization of strategies and rules. 

        3. Explain your thought process and steps you take in verifying a trig identity.  Do not use a specific example, but speak in general terms of what you would do no matter what they give you.

• From what I have learned through all my practice in this unit, verifying trig identities is all about knowing the right first step. It doesn't really matter if you mess up the next steps because you can start again but as long as you get a good start on where to go in a trig identity, you are given options on what to do next. I also pay attention to what I have to verify to so I can keep in mind what identities to use in the problem. The most important detail about what goes through my head when solving this problem is that I cannot over-complicate it. If I do over-complicate a problem, not only am I going in the wrong direction, but I exhaust myself trying to think of ridiculous ways to finish the problem. The steps should be simple, straightforward, and in the right direction.