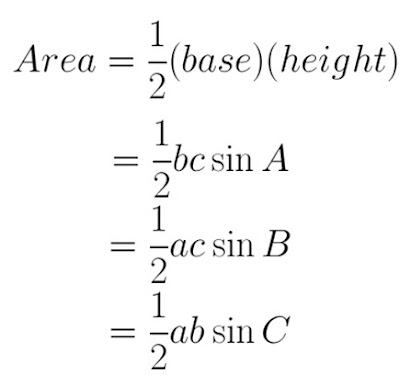SP #7: Unit Q Concept 2: Finding all trig functions using idenitites

Please see my SP7, made in collaboration with Michael C. who is incredible with coming up middle nicknames by visiting their blog post here. Also be sure to check out all the other crazy blog posts and his WPP story because it's funny on his blog here.

I/D #3: Unit Q Concept 1: Pythagorean Identities

Inquiry Activity Summary


1.       The Pythagorean Identity comes from a derivation of the Pythagorean Theorem and we can basically call it an identity because it is a proven fact, which will be shown later in the work.

        From this picture we have the standard Pythagorean Theorem and we will be replacing it with trig functions. We use the values of sine and cosine in the side values and we use the hypotenuse of r which will always equal 1. We know this because we are solving with values from a unit circle. We then see that we can the whole thing by r which will basically leave it in the form known as one of the Pythagorean Identities. We then use 45° angle to prove this identity and thus fulfilling its definition, but how do we find the other two?


2.       The other two identities are found in just a few easy steps or rather one step and a few glances at the identities chart.

       As you can see we are really only dividing by sine or cosine and figuring out what each value produces in terms of different identities. So for example in the first part where we are trying to derive for the secant and tangent one, we find that tangent equals sin over cosine. 

Inquiry Activity Reflection

1. The connections that I see between Units N, O, P, and Q so far are that when we are deriving for these identities, we use values found on the unit circle from Unit N like the radius always equaling 1 which is very convenient for us. I also see a connection between P and Q because of the way we are deriving things from one to another reminds me of how we get the Law of Cosines and Law of Sines. It may seem like they are two entirely different things but they are actually connected together with a little math. 

2. If I had to describe trigonometry in three words, they would be connectable mathematical equations. 

WPP #13-14: Unit P Concepts 6-7: Law of Sine and Law of Cosine

This WPP13-14 was made in collaboration with Michael C. from the same class.  Please visit the other awesome posts on their blog by going here

Create your own Playlist on LessonPaths!

BQ #1: Unit P Concepts 3-4: Deriving Law of Cosines and Area of an Oblique Triangle

3. Law Of Cosines Derivation 

(http://www.regentsprep.org/Regents/math/algtrig/ATT12/cosineprooof.gif)

          We need the Law of Cosines because it tells us the information of a non-right triangle for a SAS triangle, or a triangle that gives us two sides and the included angle, and a SSS triangle or a triangle that gives us all three sides. Lets take a look at the triangle above, we have cut it in half and we get two right triangles and we want to find the value of side a. If we imagine the triangle on a coordinate plane, we can use the distance formula to solve for side a. The distance formula of course asks for the coordinates of the two endpoints of whatever it is you are trying to find the actual distance of. In this case we need to find the coordinates of B and C.

(http://geometry.jdeer.com/Images/c1/distance%20formula.gif)

              So lets start by trying to figure out what coordinates we have in the next picture, 

(http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm)

                This actually shows the Pythagorean part of the derivation but we find the coordinates easily. Here we have c sin A squared and b - cos A squared because we only want that specific side when we will be using the Pythagorean Theorem (remember we can do this because we cut the triangle into two right triangles). If you wondered where are the coordinates, they are right there, its just that when we are on the coordinate plane, we are on the x-axis, so we really only care about the x value. We get the value of h from cSin a and the value of the section of b we want with b - cosA. Once we finish the math we get a value in parentheses that is sin squared A + cos squared A which equals to 1 so we can get rid of it. The final answer is what we use in the Law of Cosines. 

Still confused? Watch this video for extra help. 

4. Area Formula of an Oblique Triangle 

              The area of an oblique triangle is derived using trig functions and is drawn in a way that has one right triangle to make things a bit easier. 

(http://www.compuhigh.com/demo/lesson07_files/oblique.gif)

             The area of a triangle as we all know is half its base times its height. When we use trig functions on the triangle on the left, we know that h = asinC because sinC = h/a. Keep in mind that the h will not be automatically drawn on any oblique triangles, we are just imagining the line to help us derive.The same goes for the triangle on the right but this time we use sinA = h/c and we move around the formula as needed. So now that we have the value of our h we can just substitute it into our regular formula and we get the following three formulas depending on what we have. 

(https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiqg4S7zFlFk0GozJ6ujSgnRxQY5zRfAXuo2TlCVQDk0tBJ1p3a6-u-O6VIFiC8SjiwANZRboW_nPoWwaeEYYXzIDRlxL_DSDyxhsPOhQfwdvlNAAVMdvECHei2zZGeIirz5so1bIPuGzg/s400/hi.bmp)

Notice that we substitute the height correctly by what they give us, so we need to pay special attention to what sides they give us in order to find the area. 

References: 

http://www.algebra.com/algebra/homework/Trigonometry-basics/THEO-2012-01-16.lesson

http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm

http://www.compuhigh.com/demo/lesson07_files/oblique.gif

http://geometry.jdeer.com/Images/c1/distance%20formula.gif

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiqg4S7zFlFk0GozJ6ujSgnRxQY5zRfAXuo2TlCVQDk0tBJ1p3a6-u-O6VIFiC8SjiwANZRboW_nPoWwaeEYYXzIDRlxL_DSDyxhsPOhQfwdvlNAAVMdvECHei2zZGeIirz5so1bIPuGzg/s400/hi.bmp

http://www.youtube.com/watch?v=_DR0BfWh5Jk

http://www.regentsprep.org/Regents/math/algtrig/ATT12/cosineprooof.gif

WPP# 12: Unit O Concept 10: Angle of Depression and Elevation

Create your own Playlist on LessonPaths!

I/D #2: Unit O: Concepts 7-8: Deriving the SRTs

Inquiry Activity Summary

1. 30-60-90

             To follow this image, view from right to left starting with what we were given first, an equilateral triangle with sides all equaling 1. Since it's an equilateral triangle, we will also have all angles equal to 60°. We cut the triangle down it's altitude because we want to have right triangles, in this case we get two of them but notice that one of the angles is now 30°, one of the sides is unknown, which happens to be the longer leg, and the shorter leg has been halved to 1/2. 

            To find the unknown side, we use the Pythagorean theorem  but instead of using 1/2 we should double it so that we can have an easier time solving for it. We can do this because the triangle would still hold proportionate to a 30-60-90 as long as we double the other known side. We find the unknown side to be √3 and we set up our values into a special ratio for our special right triangle by putting n into the values so it can fit any 30-60-90 triangle as long as it fits the ratio. 

2. 45-45-90

              Once again start with what we were given, this time a square with all sides equaling 1 and the angles each being 90°. We cut across this square to get our two right triangles, both having sides equaling 1 and having two 45° angles but now their hypotenuse has an unknown value. To find this unknown value you use the Pythagorean Theorem and you get √2. We have our final values and turn them into the special ratio for our 45-45-90 triangle by using n as a variable for any other special right triangles we may have to make sure the sides correspond to the ratio of 1, 1, and radical 2.

          

Inquiry Activity Reflection

1. Something I never noticed before about special right triangles is that they can be constructed from other shapes. To go into more detail I just thought they were weird triangles that had special rules attached to them but they actually appear in a lot of places. 

2. Being able to derive these patterns myself aids in my learning because it gives me an idea of where these special rules come from and how they come together.