 |
| (http://www.regentsprep.org/Regents/math/algtrig/ATT12/cosineprooof.gif) |
We need the Law of Cosines because it tells us the information of a non-right triangle for a SAS triangle, or a triangle that gives us two sides and the included angle, and a SSS triangle or a triangle that gives us all three sides. Lets take a look at the triangle above, we have cut it in half and we get two right triangles and we want to find the value of side a. If we imagine the triangle on a coordinate plane, we can use the distance formula to solve for side a. The distance formula of course asks for the coordinates of the two endpoints of whatever it is you are trying to find the actual distance of. In this case we need to find the coordinates of B and C.
 |
| (http://geometry.jdeer.com/Images/c1/distance%20formula.gif) |
So lets start by trying to figure out what coordinates we have in the next picture,
 |
| (http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm) |
This actually shows the Pythagorean part of the derivation but we find the coordinates easily. Here we have c sin A squared and b - cos A squared because we only want that specific side when we will be using the Pythagorean Theorem (remember we can do this because we cut the triangle into two right triangles). If you wondered where are the coordinates, they are right there, its just that when we are on the coordinate plane, we are on the x-axis, so we really only care about the x value. We get the value of h from cSin a and the value of the section of b we want with b - cosA. Once we finish the math we get a value in parentheses that is sin squared A + cos squared A which equals to 1 so we can get rid of it. The final answer is what we use in the Law of Cosines.
Still confused? Watch this video for extra help.
4. Area Formula of an Oblique Triangle
The area of an oblique triangle is derived using trig functions and is drawn in a way that has one right triangle to make things a bit easier.
 |
| (http://www.compuhigh.com/demo/lesson07_files/oblique.gif) |
The area of a triangle as we all know is half its base times its height. When we use trig functions on the triangle on the left, we know that h = asinC because sinC = h/a. Keep in mind that the h will not be automatically drawn on any oblique triangles, we are just imagining the line to help us derive.The same goes for the triangle on the right but this time we use sinA = h/c and we move around the formula as needed. So now that we have the value of our h we can just substitute it into our regular formula and we get the following three formulas depending on what we have.
Notice that we substitute the height correctly by what they give us, so we need to pay special attention to what sides they give us in order to find the area.
References:
http://www.algebra.com/algebra/homework/Trigonometry-basics/THEO-2012-01-16.lesson
http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm
http://www.compuhigh.com/demo/lesson07_files/oblique.gif
http://geometry.jdeer.com/Images/c1/distance%20formula.gif
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiqg4S7zFlFk0GozJ6ujSgnRxQY5zRfAXuo2TlCVQDk0tBJ1p3a6-u-O6VIFiC8SjiwANZRboW_nPoWwaeEYYXzIDRlxL_DSDyxhsPOhQfwdvlNAAVMdvECHei2zZGeIirz5so1bIPuGzg/s400/hi.bmp
http://www.youtube.com/watch?v=_DR0BfWh5Jk
http://www.regentsprep.org/Regents/math/algtrig/ATT12/cosineprooof.gif
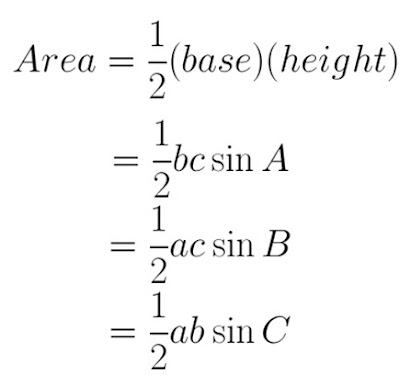
No comments:
Post a Comment